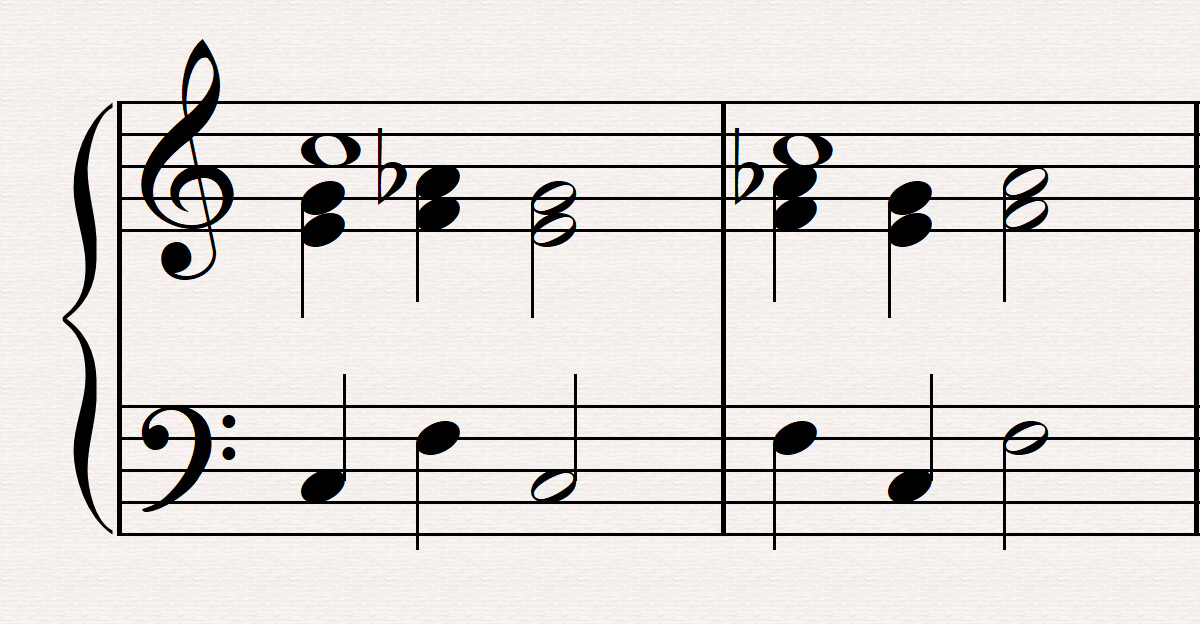Miksi molli on surullinen – osaako musiikinopettaja vastata?

Miksi duuri on iloinen ja molli surullinen? Miksi asteikossa on seitsemän säveltä? Miksi terssi kuulostaa kauniilta mutta sekunti riipii korvia? Miksi dominanttisointu pyrkii toonikaan? Tällaiset asiat kuuluvat musiikintutkimuksen eli musikologian tutkimuskenttään; musiikin havaitseminen, musiikin psykologiset vaikutukset sekä niiden syyt.

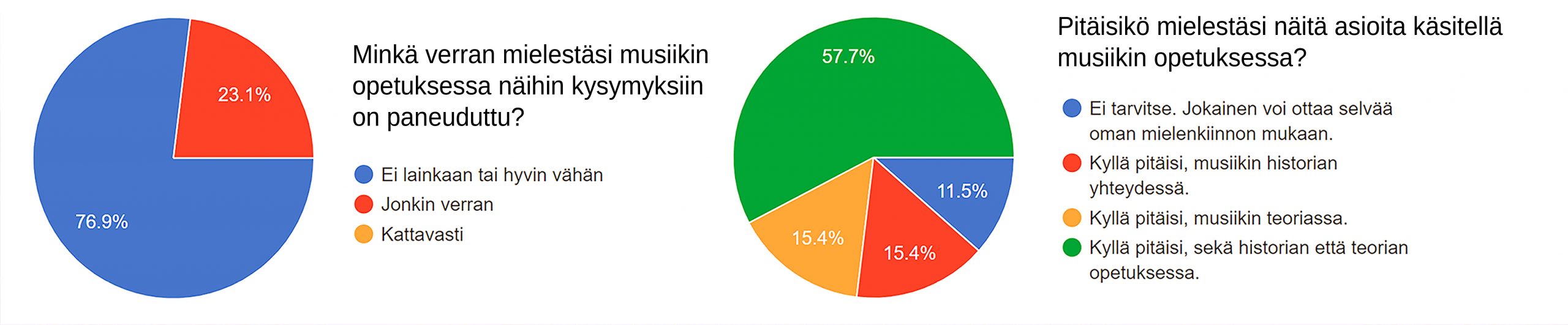
Kuuntelemme musiikkia, opiskelemme musiikin teoriaa ja säveltapailua ja opimme ymmärtämään kuinka musiikin lainalaisuudet toimivat. Mutta meille ei selitetä miksi. Saman kyselyni mukaan selvä enemmistö (lähes 80%) musiikin opiskelijoista kokee, että heille on selitetty musiikin kognitiivisia funktioita hyvin vähän tai ei lainkaan (Liite 1)!

Kuva 1. Kyselyn tulokset.

Toisaalta yli 60% on törmännyt näihin pohdintoihin musiikinopetuksen ulkopuolella. Tietoa siis vaikuttaisi olevan saatavilla. Ja vaikkei olisikaan, eikö musiikin opetuksessa – erityisesti musiikkipedagogian opetuksessa – olisi vähintäänkin syytä keskustella erilaisista teorioista asteikkojen, sointujen ja muiden musiikin elementtien emotionaalisten funktioiden takana? Eikö ole helpompaa opettaa musiikin ilmiöitä tuleville oppilaille, jos itse myös osaa tarjota selityksiä näille ilmiöille?

Musiikin polaarisuuden historiaa

”Since Renaissance emotional power of music was gradually accepted”, sanoo Leonid Perlovsky kirjassaan Music, Passion, and Cognitive Function. Musiikki vaikuttaa tunteisiin, ja monet säveltäjät osaavat käyttää musiikillisia työkaluja ohjatakseen kuulijan emootioita haluamaansa suuntaan. Esimerkiksi Dmitri Tymoczko kuvaa sävellystyötään näin:  When composing, I make various choices about chords, scales, rhythm, and instrumentation to create feelings of tension, relaxation, terror, and ecstasy, to recall earlier moments in the piece or anticipate later events” (2011, 22).

Artikkelissaan The cognitive function of music Perlovsky täsmentää: Music is different from other arts in that it affects emotions directly (2014).

Se, että muusikot ja säveltäjät tietävät, miten iloista, surullista, mahtipontista tai henkevää musiikkia tuotetaan, ei vielä tarkoita, että he tietäisivät miksi tietyt musiikin elementit vaikuttavat. ”Musiikki eroaa muista taidemuodoista sikäli, että se vaikuttaa tunteisiin suoraan (ei käsitteiden kautta)” (Perlovski 2014, suom. Keitel). Onko vaikutus puhtaasti mekaaninen; onko tietyillä sävelkuluilla, intervalleilla ja soinnuilla tiettyjä fysikaalisia vaikutuksia, jotka selittävät niiden kognitiiviset vaikutukset? Perlovskyn mielestä näin ei ole: “Pleasure from musical sounds is not merely physical and not confined to the ear… And today, the cognitive function of music remains little known among musicologists; it continues to provoke disputes, embarrassment and confusion.”

Erkki Lehtiranta on samaa mieltä: ”Musiikin havaitsemista ja kokemista ei voida yksiselitteisesti ilmaista fysikaalisilla mittareilla ja suureilla, koska ihmisen oma tietoisuus ja kokemusmaailma ovat läsnä jokaisessa kuulotapahtumassa” (2004, 15).

Duurin ja mollin polaarisuus on yksi länsimaisen musiikin vahvimpia ilmiöitä. Ironista kyllä, se on myös vähiten selitettyjä musiikin ominaisuuksia. Aihetta on käsitellyt syvällisesti Siegmund Levarie, joka International Journal of musicology -lehden artikkelissaan Musical Polarity: Major and Minor käy läpi musiikin polaarisuuden tutkimuksen historiaa ja esittelee sitten omat näkemyksensä aiheesta (1992).

Tiesitkö, että sanat dur ja moll ovat saksaa ja tarkoittavat kovaa ja pehmeää? Kova mielletään helposti maskuliiniseksi, pehmeä feminiiniseksi ominaisuudeksi. Jo käsitteissä siis annetaan näille kahdelle musiikkiasteikon perustyypille abstraktit sisällöt, joita on hyvin vaikea perustella teoreettisesti.

Levarie mainitsee duurin ja mollin vastakkaisuutta selittävät kaksi teoriaa. Yhden teorian mukaan ne ovat ”tasa-arvoisia mutta vastakkaisesti latautuneita voimia, yleisen polariteettiprinsiipin musikaalinen ilmentymä”. Toisen teorian mukaan ”duuri on luonnollinen ilmiö, joka tarjoaa perusmateriaalin musiikin rakentamiseen, kun taas molli on keinotekoinen, ymmärrettävissä ainoastaan duurille alisteisena.” (Levarie 1992, 29.)

Artikkelinsa loppupuolella Levarie paljastuu duuri-molli-paria koskevan ensimmäisen teorian vahvaksi kannattajaksi. Ja tunnustan, että tämä tekee minusta Levarien vahvan kannattajan: Mielestäni duurin ja mollin polaarisuus on maailmassa yleisesti vaikuttavan dualistisen vastakohtaisuuden ilmentymä. Sama polaarisuus ilmenee musiikissa mm. pareissa maallinen/henkinen, pop/taide, kaksijakoinen/kolmijakoinen.

Jos ajatellaan, että dualistinen polaarisuus on jonkinlainen universaali luonnonlaki, joka näin olleen väistämättä ilmenee myös musiikissa, voisivatko muutkin musiikin ominaisuudet olla heijastumia vastaavista universaaleista laeista. Ainakin länsimaisen musiikinteorian varhainen uranuurtaja Pythagoras ajatteli näin: ”Pythagoras tutki kaiken luomisen takana olevia yksinkertaisia matemaattisia lukusuhteita, pyhän geometrian perusrakenteita ja vastaavuuksien universaalia lakia, tuota hermeettistä aksioomaa…” (Lehtiranta 2004, 48). Hermeettinen periaate tunnetaan parhaiten sananparresta ”niin ylhäällä, kuin alhaalla”. Sen mukaan kaikki fyysisen maailman ilmiöt heijastavat jonkinlaista kosmista geometrista rakennetta.

Mutta jos musiikin vaikutuksia aletaan selittää tällaisen kosmologian kautta, mennään kovasti filosofisille, jopa esoteerisille tai uskonnollisille taajuuksille. Tekemäni kyselyn mukaan useimmat musiikkia opiskelleet kuitenkin ovat hyvin kiinnostuneita tästä alueesta, ja peräti 90% on sitä mieltä, että näitä musiikin filosofisia kysymyksiä pitäisi käsitellä joko musiikinteoriassa tai -historiassa (Liite 1).

Yläsävelsarja

Levarien esittelemä toinen teoria, jonka mukaan duurin on luonnollinen ja molli keinotekoinen asteikko, löytää hänen artikkelissaan perustelun yläsävelsarjasta. Hän lainaa mm. Rameauta, jonka mukaan duuriasteikon sävelet löytyvät perussävelen pohjalta harmonisesti ja mollin sävelet aritmeettisesti. Harmoniset sävelet ovat perussävelen yläsäveliä, jotka todella soivat, kun taas aritmeettiset sävelet ovat ns. alasäveliä, jotka ovat vain teoreettisia. (Levarie 1992, 35.)

Muistan, että yläsävelistä puhuttiin lyhyesti musiikinteorian peruskurssitasolla. Aihetta ei kuitenkaan selkeästi linkitetty musiikin funktioihin, duuri-molli-polariteetin selittämisestä puhumattakaan. Jos kaiken länsimaisen musiikin kulmakivi duuriasteikko perustuu yläsävelsarjaan, kyseessä vaikuttaisi kuitenkin olevan melko tärkeä aihe!

Erkki Lehtiranta kertoo, että ”Pythagoras oivalsi soittimen kielen pituuden täsmällisen suhteen sävelen korkeuteen. Hän kokeili monokordilla eli yksikielisellä soittimella ja laski konsonoivien intervallien perustavat numeeriset suhteet. Näin luotiin pohja länsimaiselle musiikinteorialle.” Hieman myöhemmin hän jatkaa: ”Harmonisimmat sävelet syntyvät yksinkertaisimmista lukusuhteista. Ne tuottavat konsonanssit, sopusointuiset sävelyhdistelmät, kun taas monimutkaiset lukusuhteet tuottavat dissonanssit, epäsointuisuudet” (2004, 49).

Duurin konsonanssisävelet ja niitä vastaavat värähtelysuhteet löytyvät yläsävelsarjan alkupuolen sävelistä; kvintti (3/2), kvartti (4/3) terssi (5/4) ja seksti (5/3). Lievästi dissonanssiset käänteisintervallit suuri sekunti ja pieni septimi soivat suhteissa 9/8 ja 16/9 (käänteisintervalli saadaan, kun alempi sävel nostetaan oktaavilla). Pythagoraan logiikka toimii; yksinkertaisimmat lukusuhteet tuottavat sopusoinnun, monimutkaiset riitasoinnun. Miksei tätä ilmeisen helposti ymmärrettävää asiaa sisällytetä musiikinopetukseen? Se selittää loogisesti konsonanssin ja dissonanssin välisen eron!

Oman tutkimukseni mukaan (liite 2) mollikolmisointu on yläsävelsuhteista johtuen todellakin dissonanssisempi – mutta vain hieman. Aivan vakuuttavaa perustelua yläsävelistä ei siis löydy duurin ylivertaisuudelle mollin rinnalla – eikä molliasteikon surullisuudelle.

Johtosävelet ja Tritonus musiikin funktioiden selittäjänä

Musiikinteoriassa opetetaan, että johtosävelet ovat diatonisia säveliä, jotka ovat puolisävelsuhteessa joko alempana tai ylempänä sijaitsevaan toiseen asteikon säveleen. Mutta miksi tällaisia johtosäveliä on ja miksi niillä on tällaiset taipumukset?

Taipumus ei tule missään niin vahvasti esille kuin tritonusintervallin (ylinouseva kvartti) pyrkimyksessä purkautua. Tritonuksen vahvaa yhteyttä johtosäveliin selittää Jerry Tachoir: Tritonus on kaikkien dominanttisointujen karaktääri-intervalli, jonka luovat ”johtosävelet” eli terssi ja septimi. Tritonus voi purkautua kahdella vastakkaisella liikkeellä, toisessa molemmat nuotit liikkuvat sisään päin puoliaskelen verran, toisessa molemmat nuotit liikkuvat ulos päin puoliaskelen verran. Tämä tritonuksen purkautuminen on tyypillistä perinteisessä länsimaisessa harmoniassa, kun V7-sointu purkautuu I sointuun. (Tachoir 2000, 40.)

Niinpä esim. C-duurin sisältämä ainoa tritonus sävelten H ja F välillä purkautuu oikeaoppisesti (ja samalla miellyttävän kuuloisesti) sisään päin; H ylös C:hen ja F alas E:hen.  Tästä seuraa kyseisen sävellajin dominanttisoinnun G7 pyrkimys purkautua toonikasointuun C. Purkaantumissääntö on sekä klassisen että jazz-teorian ”peruskauraa”, ilmiön selitys ei ole.

Tritonus on sekä duuri- että molliasteikon varsinainen musta lammas, sitä onkin sanottu ”paholaisen intervalliksi”, mikä johtunee sen sangen riitaisasta soinnista. Löytyykö selitys jälleen yläsävelsarjasta? Diatonisen tritonussävelen (suhde 45/32) ja yläsävelasteikkoon pohjautuvan tritonussävelen (11/8) välillä on korvin kuultava ”paholaismainen” ristiriita.

John Sloboda, musiikin psykologian professori Lontoon Guildhallin musiikin ja draaman koulusta selittää tritonuksen funktiota taipumuksellamme etsiä musiikista jännitteen purkautumista. Burnsin (2016) mukaan Sloboda on esittänyt: ”Aivomme on viritetty hakemaan odottamaamme musiikkia, ja yleensä musiikki on enemmän konsonanssista kuin dissonanssista, joten odotamme mukavaa sointua. Joten kun sointu ei olekaan aivan mitä odotamme, se aiheuttaa sinussa hienoisen emotionaalisen kitkan, koska se on omituinen ja odottamaton.”

Levarie viittaa Goethen ja säveltäjä Karl Zelterin esittämään vastaavaan näkemykseen: Perussävel C:n yläsävelet synnyttävät C-duurin, alasävelet F-mollin. Duuri on peräisin nousevasta liikkeestä, jossa intervallit laajentuvat huippua kohti. Molli taas on peräisin laskevasta liikkeestä, jossa intervallit laajentuvat pohjaa kohti. (1992, 41.) Hän itse perustelee tätä myös johtosävelillä, kun C-duuri- ja F-mollisointu vuorottelevat: Kummassakin kolmisoinnun muodossa [duuri ja molli] terssisävel toimii johtosävelenä – ylös päin duuridominantissa (H:sta C:hen), alas päin mollisubdominantissa (As – G)” (1992,41).

Kuva 2. C-Fm-purkaukset.

Mikä mielenkiintoisinta, tämä ”selittää, miksi korotettu septimi lainataan molliin ja alennettu seksti duuriin!!”. Yhdyn tässä kohtaa täysin rinnoin Levarien huutomerkkeihin, samoin kuin hänen nasevaan jatkotokaisuunsa: ”Jos tätä ei vastaavasti tunnusteta, syy on tietämättömyys polariteettijärjestelmästä”. Pop/jazz-musiikinteoriassa, jota olen itse opiskellut korkeakoulutasolla, dominanttisoinnun duuriterssin lainaaminen harmoniseen tai melodiseen molliin sekä mollisekstin lainaaminen duuriin ovat keskeisiä ilmiöitä, mutta niitä ei meillekään teorian tunneilla selitetty, vaikka Levarien tarjoama selitys on musiikillisesti ja filosofisesti erittäin looginen ja tuntuu intuitiivisesti oikealta.

Duuriasteikon käänteisasteikko, jossa kaikki koko- ja puolisävelaskelet ovat käänteisessä järjestyksessä, on fryyginen molliasteikko – kenties parhaiten tunnettua aiolista (luonnollista) molliasteikkoakin ”surullisempi”. Sen molemmat johtosävelet pyrkivät luontevasti alas päin; molliseksti viidenteen säveleen ja matala sekunti ensimmäiseen – siispä duuri pyrkii ylös päin, molli alas!

Levarie ei perustele duurin nousujohtoisuudella ja mollin laskujohtoisuudella niiden iloisuutta ja surullisuutta, mutta itse olisin taipuvainen näin tekemään. Polaarisista vastapareista alas-ylös, sisään-ulos, taakse-eteen ja myös tumma-vaalea voidaan nähdä vastaavina. Esimerkiksi kuvasommittelun psykologiassa yläviistoon suuntautuva liike nähdään samalla optimistisena. Näin ollen tuntuisi samalla tavalla johdonmukaiselta, että johtosävelten vuoksi luontevammin ylös päin suuntautuva duuri on optimistisempi (iloisempi) kuin laskeutuvaan liikkeeseen taipuvaisempi molli.

Tämä sopii yleiseen polaariseen prinsiippiin, jota Kiinan taolaisuudessa kuvaa Jin- ja Jang-energioiden vastakohtaisuus. Sen yleisesti tunnetussa musta kuvaa vastakohtien sisään päin suuntautuvia tummia ulottuvuuksia ja valkoinen vastaavasti ulos suuntautuvia vaaleita ulottuvuuksia. On hauska havaita, että iloinen ”jang-asteikko” C-duuri sisältääkin kaikki pianon valkoiset koskettimet ja surumielinen ”jin-asteikko” fryyginen C-molli kaikki mustat koskettimet!

Kirjoittaja

Veli Martin Keitel
Musiikkipedagogin tutkinto-ohjelma 2020
Jyväskylän ammattikorkeakoulu

Lähteet:

Burns, J. 2016.A Brief History of the Devils Tritone. Mentalfloss.com, March.
Lehtiranta, E. 2004. Musiikin korkeammat oktaavit. Dialogia Oy.
Levarie, S. 1992. Musical Polarity: Major and Minor. International Journal of Musicology 1.
Perlovsky, L. 2017. Music, Passion, and Cognitive Function. Academic Press.
Perlovsky, L. 2014. The Cognitive Function of Music. Interdisciplinary Science Reviews, June.
Tachoir, J. 2000. The Devil’s Interval. Percussive notes magazine, December.
Tymoczko, D. 2011. A Geometry of Music. Oxford University Press.

Liite 1: Miksi molli on surullinen – pitäisikö musiikinopettajan tietää? – google forms-kysely